| УДК 631.16:658.155
* ДИСКРИМИНАНТНАЯ МОДЕЛЬ | ПРОГНОЗИРОВАНИЯ ФИНАНСОВОГО I СОСТОЯНИЯ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ПРЕДПРИЯТИЙ
М.А. КОЗЛОВА, кандидат технических наук, доцент Л.В. КЛИМКИНА, кандидат экономических наук, доцент (ФГБОУ ВПО «Костромская ГСХА») Е.П. СМИРНОВА, специалист
(Территориальный орган Федеральной службы государственной статистики по Костромской области)
Проблема диагностики и прогнозирования финансового состояния предприятия до сих пор остается одной из главных в современной экономике России. К настоящему времени достигла большой остроты очень серьезная проблема хронической неплатежеспособности, огромной задолженности сельскохозяйственных организаций, значительная часть которых в результате своей деятельности несет огромные убытки и не может обеспечить даже простого воспроизводства. Специфика российских условий и их отличия от стран с развитой экономикой требуют, чтобы модели прогнозирования риска финансовой несостоятельности учитывали как особенности отрасли, так и структуру капитала предприятия.
Процесс разработки модели прогноза несостоятельности отличается от разработки классификационной модели по цели исследования [2], в результате чего существует ряд определенных требований к анализируемой информации. В то время как целью анализа является установление совокупности показателей и их значений, позволяющих определить принадлежность хозяйства к какой-либо группе по уровню финансового состояния, то в данном слу-
чае в качестве итогового показателя принят не уровень финансового состояния, а само наличие процедуры банкротства.
В ходе разработки многомерной прогностической модели решались следующие частные задачи:
- определение группы наиболее информативных показателей для возможности прогнозирования состояния предприятия(банкрот - не банкрот);
- построение математической модели прогноза ухудшения финансового состояния предприятия.
Для исследования были отобраны годовые отчеты 104 сельскохозяйственных организаций за 2009 год. В 52 из них впоследствии (в 2010-2013 гг.) была введена процедура конкурсного производства, остальные 52 по состоянию на 1 января 2013 года являлись действующими предприятиями с различной степенью устойчивости финансового состояния.
Для анализа данных была использована следующая совокупность переменных: х1 - быстрый коэффициент ликвидности; х - коэффициент покрытия запасов; х3 - текущий коэффициент ликвидности; х4 - коэффициент финансовой зависимости; х5 - коэффициент автономии собственных средств; х6 - коэффициент
2,0 1,5 1,0 0,5 0,0 -0,5 -1,0 -1,5
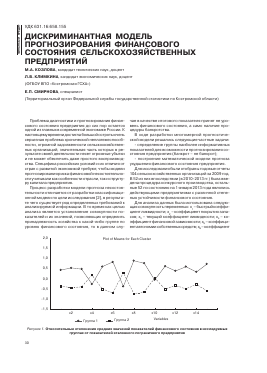
Plot of Means for Each Cluster
х2 х4 х6 х8
-о- Группа 1 -□- Группа 2
х10 х12
Variables
х14
Рисунок 1. Относительные отклонения средних значений показателей финансового состояния в исследуемых группах от показателей эталонного пограничного предприятия
Показатели статистики переменных
Переменные Лямбда Уилкса Частная лямбда Р-исключение Уровень значимости Р-критерия (Р) Коэффициент корреляции (г) Уровень толерантности (Т)
Х3 0,271323 0,615418 56,86705 0,000000 0,771586 0,228414
Х5 0,208208 0,801973 22,47022 0,000008 0,835530 0,164470
Х8 0,317580 0,525779 82,07638 0,000000 0,230311 0,769689
Х„ 0,200385 0,833283 18,20664 0,000048 0,262995 0,737005
9
о. £
О
X <
Таблица 2
Итоги анализа дискриминантной функции
Наименование статистики Значение статистики
Собственное значение дискриминантной функции 4,999
Каноническая корреляция 0,913
Лямбда Уилкса 0,167
Статистика %2 164,670
Степень свободы 4
Уровень значимости 0,000
Таблица 3
Классификационная матрица
Группа Предсказанная принадлежность к группе Итого
1 2
Частота 1 20 5 25
Исходные 2 2 23 25
% 1 80 20 100,0
2 8 92 100,0
обеспеченности запасов собственными оборотными средствами; х7 - индекс постоянного состава; х8 - коэффициент оборачиваемости активов; х - коэффициент оборачиваемости кредиторской задолженности; х10 - коэффициент оборачиваемости дебиторской задолженности; х11 - коэффициент оборачиваемости запасов; х12 - общая рентабельность; х13 - рентабельность активов; х14 - рентабельность собственного капитала; х15 - рентабельность продукции (продаж) [2].
На рисунке 1 представлены относительные отклонения средних значений показателей каждой группы предприятий от эталонного пограничного предприятия.
Как видно из рисунка 1, большинство значений показателей в выделенных группах существенно отличаются.
В ходе пошагового дискриминантного анализа с исключением были выделены четыре переменные, наиболее точно отражающие степень разделения двух исследуемых групп: - текущий коэффициент ликвидности (х^); коэффициент автономии собственных средств (х5); коэффициент оборачиваемости активов (х8); коэффициент оборачиваемости запасов (х11).
На основании выявленных переменных были построены две линейные функции классификации предприятий:
= 3,26х3 + 29,786х5 + 14,401х8 - 0,847х11 - 22,99;
Ъ2 = 0,512х3 + 16,15Х5 - 1,771х8 + 3,133х11- 7,052.
Группу, в которую вошли организации - банкроты, характеризует функция Ъ2. Соответственно, любое ис-
следуемое в дальнейшем предприятие будет являться потенциальным банкротом, если рассчитанный по его данным показатель второй функции будет выше аналогичного показателя первой функции.
Качественная характеристика переменных, определяющих классовую принадлежность объекта исследования, представлена в таблице 1.
Все переменные нашей модели являются существенными. Об этом свидетельствуют значения частных лямбда, характеризующих вклад каждой переменной. Показатели исключения Р-критериев и их уровни значимости говорят о невозможности исключения каких-либо критериев.
Наибольшая разделительная способность отмечена у переменной Х8. Этот финансовый индикатор имеет наименьшее значение показателя частной лямбды, при этом рассматриваемая переменная обладает наибольшим значением Р-критерия при наименьшем уровне его значимости.
В результате анализа получена каноническая линейная дискриминантная функция, имеющая вид:
Ъ = 0,622х3 + 3,084х5 + 3,658х8 - 0,9х11 - 3,549.
Анализ значимости дискриминантной функции позволяет говорить о степени разделительных свойств модели. Основные показатели статистики, характеризующие дискриминантную модель, представлены в таблице 2.
Разработанная модель обладает хорошей разделительной способностью. Об этом свидетельствует
Рисунок2. Распределение значений функции в группах
достаточно высокое значение собственного числа дискриминантной функции. Полученный коэффициент канонической корреляции определяет высокую степень зависимости между массивом значений переменных, включенных в функцию, и рассматриваемым множеством групп. Статистика^, равная 164,67, при уровне значимости 0 говорит о значимости функции и наличии различий между исследуемыми группами. Значение статистики лямбды Уилкса, равное 0,167, при значении Р-критерия (с числом степеней свободы 4 и 91), равным 113,5, и уровне его значимости (р), равном нулю с точностью до 4 знаков после запятой, говорит о корректности проведенной дискриминации.
Для определения прогнозной способности модели был проведен расчет значений функции по исследуемой выборке организаций на основании годовых бухгалтерских отчетов за 1 год до инициации процедуры банкротства.
Критическое значение индекса Ъ равно 0. С этой величиной сопоставляется расчетное значение показателя канонической линейной дискриминантной функции для конкретного предприятия, что позволяет высказать суждение о возможном банкротстве пред-
приятия в ближайший год (Ъ<0) или о его достаточно устойчивом финансовом положении (Ъ>0). Значение Ъ=0 является зоной неопределенности, в этом случае имеется одинаковая вероятность обоих результатов исхода (см. рисунок 2).
Первоначальная дискриминация на данных обучающей выборки предприятий показывает высокую результативность модели: 100% правильной дискриминации.
Количество и процент корректно классифицированных предприятий в результате дальнейшей кросс-проверки модели на данных предприятий, не участвующих в обучающей выборке, представлены в таблице 3.
Результаты последующей кросс-проверки модели показали, что с достаточно высокой вероятностью (92%) можно утверждать, что при попадании значения Ъ в интервал (-~;0) предприятие при условии продолжающегося ухудшения его положения обанкротится. Также с достаточно высокой вероятностью (80%) можно утверждать, что при попадании Ъ в интервал (0;+~) несостоятельность предприятию не грозит. Ошибочные результаты можно объяснить тем, что дискриминирующая функция является линейной, в связи с этим данные предприятий, находящиеся на границе обла-
Таблица 4
Расчет классификационной модели для СПК Колхоз «Родина»
Показатели 2009 г. 2010 г. 2011 г. 2012 г. 2013 г.
Коэффициент промежуточной ликвидности (х1) 0,161 0,211 0,271 0,364 0,504
Текущий коэффициент ликвидности (х3) 2,277 2,620 3,022 2,949 3,423
Коэффициент обеспеченности запасов собственными оборотными средствами (х6) 0,305 0,426 0,489 0,450 0,553
Коэффициент оборачиваемости активов (х8) 0,535 0,542 0,505 0,480 0,391
Коэффициент оборачиваемости кредиторской задолженности (х9) 4,302 4,468 4,862 4,463 3,943
Рентабельность собственного капитала (х14) 16,961 27,224 18,923 13,792 18,396
Ъ1 = 20,660х1 + 6,945х3 - 3,386х6 + 32,457х8 - 1,096х9 -1,313х14 - 208,601 -200,11 -210,54 -197,45 -189,54 -192,07
Ъ2 = - 2,747х1 + 0,510х3 - 0,290х6 + 47,907х8 + 1,004х9 + 2,158х14 - 43,563 23,62 46,27 27,00 14,05 19,03
Ъ3 = - 0,290х1 + 0,732х3 - 0,166х6 + 19,921х8 + 0,332х9 + 1,619х14 - 10,252 30,86 47,89 34,11 25,10 30,90
Ъ4 = 0,236х1 + 0,418х3 - 0,570х6 + 10,712х8 + 0,063х9 -0,143х14 - 3^73 0,42 -0,88 0,09 0,54 -0,93
Ъ5 = 1,102х1 + 0,335х3 - 3,837х6 + 8,966х8 + 0,018х9 -3,383х14 - 8,774 -61,51 -96,46 -68,74 -51,39 -67,85
Ъ6 = 2,158х1 + 0,566х3 - 3,853х6 + 16,724х8 - 0,189х9 -31,727х14 - 58,760 -588,29 -913,98 -651,19 -488,43 -635,72
Расчет дискриминантной модели для СПК Колхоз «Родина»
Показатели 2009 г. 2010 г. 2011 г. 2012 г. 2013 г
Текущий коэффициент ликвидности (х3) 2,277 2,62 3,022 2,949 3,423
Коэффициент автономии собственных средств (х5) 0,688 0,714 0,7
Для дальнейшего прочтения статьи необходимо приобрести полный текст. Статьи высылаются в формате PDF на указанную при оплате почту. Время доставки составляет менее 10 минут. Стоимость одной статьи — 150 рублей.