УДК 517.956.223
НЕКОТОРЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЭЛЛИПТИЧЕСКОГО ТИПА СО СМЕШАННЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ
М.И. Сугаков,аспирант С.Р. Амироков, кандидат физико-математических наук Северо-Кавказский государственный технический университет Ставрополь, Россия
На примере краевой задачи гидродинамики со смешанными условиями вдоль одной из границ показано применение приближённого метода средневзвешенного потенциала, проведено сравнение решения с аналитическим и численным.
Ключевые слова: уравнение Лапласа, метод средневзвешенного потенциала, метод Хоу, конформное преобразование, эллиптический интеграл
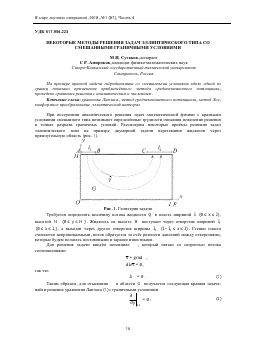
При построении аналитического решения задач математической физики с краевыми условиями смешанного типа возникают определённые трудности описания поведения решения в точках разрыва граничных условий. Рассмотрим некоторые приёмы решения задач эллиптического типа на примере двумерной задачи перетекания жидкости через прямоугольную область (рис. 1).
V
X
■ .'■■■/•// .'■ ■■• ,У А- ■■ ■V ■■ .,' .'■ .,' .'■ .,■ '
0 I Е
Рис. 1. Геометрия задачи Требуется определить величину потока жидкости Q в пласте шириной I (0 < х < I), высотой Н (0 < у < Н) . Жидкость на высоте Н поступает через отверстие шириной /1 (0 < х < /1), а выходит через другое отверстие ширины 12 (I —12 < х < I). Стенки пласта считаются непроницаемыми, поток образуется за счёт разности давлений между отверстиями, которые будем полагать постоянными и заранее известными.
Для решения задачи введём потенциал (р, который связан со скоростью потока соотношениями
ГУ = gradр, [Шуу = 0,
так что
Ар = 0. (1)
Таким образом, для отыскания р в области О получается следующая краевая задача: найти решение уравнения Лапласа (1) с граничными условиями
др
ду
= 0,
(2)
дф
ду
= 0,
ф AB = ф = const, ф = ф2 = const,
дф
ду
дф
ду
= 0.
(3)
(4)
(5)
Вдоль стороны АО действуют смешанные граничные условия (3) и (4). Один из способов решения данной задачи, основанный на методе средневзвешенного потенциала (иначе известного как метод Хоу, см. [1, 3]), заключается в следующем.
Проведём разделение переменных по методу Фурье и учтём условия (2) и (5). В результате получим общий вид решения
о Pn
гДе Pn = у; Ч,
ф(х, у) = Со + X Cn cos pnx ch РпУ >
произвольные постоянные.
(6)
Введём обозначение Сп = Q ■ Ап, где Q - величина искомого потока, после чего (6) преобразуется к виду
ф (х, у)=со+ап cos pnx ch pny •
(7)
Поток определяется как криволинейный интеграл (например, вдоль какого-либо из отверстий) от нормальной составляющей производной потенциала. В формулу для производной потенциала не войдёт постоянная С0, поэтому мы имеем право разделить все
коэффициенты Сп ряда в правой части выражения (6) на Q.
Примем значения потенциала ф при у = Н на отрезках АВ и СО в среднем равным
заданным величинам ф1 и ф2, которые будем теперь обозначать ф1 и ф2 соответственно
1
(ф)1 AB = Т Í ф(х'H )dx = ф1*'
Ч о i
1 J2
ф\CD = т Í ф(х'H)dx = ф*.
l2 l-l2
(8) (9)
(10)
Подставляя (7) в (8) и (9), получим алгебраическую систему относительно С0 и Q
С + Q-Si = j*, li
Q *
Со + fS2 = j 2, l2
где Si и S2 обозначают следующие суммы
^ i
51 =E A — ch b nH sin b Ji,
n=i b n ¥ (—i)n
52 =Z An ^ch bnH sin bnl2.
n=i bn
Чтобы отыскать неизвестные коэффициенты An, применим упрощающее предположение о том, что значения нормальных скоростей фильтрации вдоль отрезков AB и CD постоянны. Из этого получаем следующее распределение нормальной скорости на границе AD
(11)
(12)
ВС
AO
ED
n=1
n=1
F (х) = j
dy
y=h
- ^ , при 0 £ X £ l{;
A
0, при l1 < X £ l -12;
Q
—, при l -12 < X £ l. l2
pnx
Разложим F (х) в ряд Фурье по системе функций cos —— на отрезке [0, l]
F (х) = j
dy
y=H
= — + V an cos Вnx,
n ~ n >
n=1
(13)
2 Q
a0 = 0, an =——
0 n l Pn
1 ft i (-1)П • ft i - J Sin Вnl1 + Sin Вn 2
11 I ->
Дифференцирование (7) при y = H даёт формулу
dj
dy
= QV An b n cos В nX sh В nH.
(14)
y=H
Сравнивая (13) и (14), и пользуясь линейной независимостью функций cos ff nX, найдём
A = 2 1 (-1) n/: sin fnl2 -12 sin fnlx
l bl h¡2 sh ЬnH
Таким образом, числовые ряды S1 и S2 принимают вид
Si = 2 £ br ^hT^ ((-Dn l1 sin bnl2 -12 sin bJ\ )sin bJ\
l n-1 b 3
l1l2
(15)
S2 = 2 £ _13^ílbH (li sin bnl2 - (-i)ll2 Sin bnli )sin bnl2 . (16)
l n=1 b n l1l2
Нетрудно доказать абсолютную сходимость рядов (15) и (16). Если суммы известны, то величина потока находится по следующей формуле
(j2 - j* Xl:
Q = ^
S 2^1 Sj^
2
(17)
Для расчёта потока требуется иметь оценку остаточных членов рядов ^ и Б2. Получить оценку можно воспользовавшись, например, признаком Дирихле сходимости рядов Абелева типа [2]. Оценка остаточных членов обоих рядов оказывается равной
2
\г £ л —
4l (l, +12) , pH 1 2 cth-
p 3l1l2
l
J_
л
2
Другой метод построения решения основан на применении конформного преобразования, отображающего область задачи в область, для которой решение известно. В нашем случае удобно воспользоваться решением двумерной задачи об отрезках с заданными потенциалами, лежащих на оси Ох , приведённом в [3]. Опишем алгоритм решения.
1. Отобразим прямоугольную область О (рис. 1) на верхнюю полуплоскость (рис. 2). Данное преобразование осуществляется с помощью эллиптических функций (как частный случай отображения Шварца-Кристоффеля). Ради удобства, передвинем область О и отразим относительно её горизонтальной оси (что не изменит величины искомого потока), как показано на рис. 3.
1
■.-». -Уу/ ■///'. V, -у.л -у.-у
1 А,.
Ч -- Я,;, -Т
-*■, ■,<V ■
О Л' В' О с' ¿У Е'
Рис. 2. Преобразованная область
1У п О I
Рис. 3. Область С, подготовленная для конформного отображения
Найдем модуль эллиптического интеграла к0 через отношение высоты прямоугольника к половине его ширины т = 2Н/I (см. [4]).
ко = 4-
I *
1 + 21 *
где * = е
(18)
2. Пересчитаем координаты образов точек А', В', С' и О' по формуле
С = 8п| Ко у, к
(19)
в которой 2 и С - комплексные координаты точек до и после конформного преобразования, функция 8П - эллиптический синус Якоби, К0 = К(к0) - полный эллиптический интеграл
Лежандра первого рода.
В случае, приведённом на рис. 3, координаты образов точек будут равны
( 21 -1
х1 = 8п( - К0, к0) = -1, х2 = бп1 К0 —1-, к0
I
х3 = К01 22,к0|, х4 = 8П(К0,к0) = 1.
3. Найдём приток по следующей формуле (её вывод можно найти в [3, стр. 47-49]).
Q К'(к), ,
Q = ^777№ - фг\>
К(к)
(20)
к=
( х3 - х2 )( х4 - х1 )
( х4 - х2 )( х3 - х1 )
Вычисление новых координат по формуле (19) осложняется при Т = 2Н/1 < 1/6, что связано с особенностью эллиптического интеграла НшК(х) = ¥. В этом случае следует
2
2
V =0
РТ
V =1
развернуть прямоугольник АО ЕО (рис. 3) так, чтобы сторона АО лежала на оси Ох , а ось Оу делила сторону АО пополам. При этом ход решения не изменится.
Во время расчётов следует иметь в виду, что функции эллиптических интегралов К(к) , работа которых основана на методе арифметико-геометрического среднего, могут давать неправильный результат вычислений в определённом диапазоне параметра. В частности, функции еШрке пакета МЛТЬЛБ и БШрйоК инструмента WolframAlpha основаны на этом алгоритме. Для проверки можно вычислять эллиптический интеграл как сумму ряда (см. [5]).
Сравнение вышеизложенных решений, т.е. решения методом средневзвешенного потенциала (СВП) и аналитического, а также решения, получаемого при помощи метода конечных элементов (МКЭ), показало приемлемую точность решения методом СВП при А +¡2 < ¡/2. Величины потока, находимые методом СВП, оказываются ниже вычисленных аналитически, что характерно для данного метода. Величины, получаемые МКЭ, также оказываются ниже точных значений при размерах сетки 300^2600 элементов (в зависимости от размеров области).
2.6 И 2.2 2 1.8 о 1.6 М 1.3 1
08
-А:-СВП —& — АиалипивС "ое
Г /
. ^о- -о- -о- -в- в - е- в - ф
Г/?
и
1V
61
I
Ю
14
Рис. 4. Зависимость потока от высоты прямоугольного пласта
ф1 = 4 , ф2 = 1, I = 10, /1 = 2, 12 = 3
-е- -
-*-СЕП
- Амалтн11ескйЕ
/
/л
У /
1.5
ойчсГ-1
5
Рис. 5. Зависимость потока от суммарной длины отверстий
ф1 = 4, ф2 = 1, I = 10, Н = 4, 11 = ¡2.
Все решения показывают линейную зависимость потока от разности потенциалов ( — (2, о чём говорят также формулы (17) и (20). Наблюдается замедление роста потока при увеличении высоты Н (рис. 4), при переходе Н > I, высота перестаёт оказывать существенное влияние на величину потока. Погрешность метода СВП растёт при увеличении 11 +12 (рис. 5).
:
/
/
i
я
Г
F у
f
э.;
3.5 Щ ifi
Рис. 6. Погрешность решения по методу СВП в процентах.
j = 4 , j2 = 1, l = 10 , / = l2.
Рис. 7. Точность решения МКЭ от числа конечных элементов N
В целом, погрешность метода СВП уменьшается при увеличении H и растёт с увеличением /1 + /2. На рис. 6 показан график зависимости погрешности метода в процентах от высоты прямоугольного пласта и от длины отверстий /1 = /2. Отклонение результатов СВП от точных не превосходит 10-15% в случае /1 + /2 < I/2 .
Метод конечных элементов даёт заниженные значения потока в рассмотренной задаче. Наблюдается рост точности решения с увеличением числа конечных элементов (рис. 7). Решения методом конечных элементов получены с помощью COMSOL 3.4, тип уравнения -Laplace's, настройки стандартные.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
1. Фихманас Р.Ф., Фридберг П.Ш. Метод Хоу расчёта ёмкости тел и его связь с вариационными принципами // ЖТФ. - 1970. - Т.40. - вып.6. - С. 1327-1328.
2. Признак Дирихле [Электронный ресурс] : Википедия - Свободная энциклопедия : [сайт]. URL: http://ru.wikipedia.о^^Ы/Признак_Дирихле (дата обращения: 24.12.2009).
3. Иоссель Ю. Я., Кочанов Э. С., Струнский М. Г. Расчет электрической емкости. 2-е изд., перераб. и доп. СПб. : Энергоиздат. Ленингр. отд-ние, 1981. 288 с.
4. Лаврентьев М. А., Шабат Б. В. Методы теории функции комплексного переменного. - 4-е изд., перераб. и доп. М. : Наука, 1973. 749 с.
5. Двайт Г. Б. Таблицы интегралов и другие математические формулы / Г. Б. Двайт; перевод с англ. Н. В. Леви; под ред. К. А. Семендяева. 5-е изд. М. : Наука : Главная р
Для дальнейшего прочтения статьи необходимо приобрести полный текст. Статьи высылаются в формате PDF на указанную при оплате почту. Время доставки составляет менее 10 минут. Стоимость одной статьи — 150 рублей.